Parabola Blog

Another Parabola

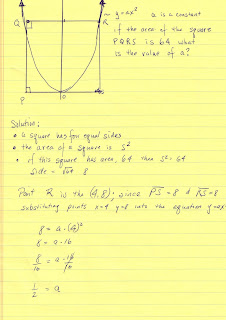
Here is another parabola problem that has a square labeled PQRS with an area of 64. The top corners intersect a parabola that sits on the bottom side.

The function of the parabola is y=ax^2

The key to solving this problelm is remember that parabolas are symmetrical. Since the square root of 64 = 8, then all sides have a length of 8. QR = 8, and so the point R is (4,8)

Substitute these two points into the equation and solve

8 = a*(4)^2

8 = a* 16

8/16 = a * 16/16 a = 1/2

Fun with Parabolas

To get a good handle on SAT parabolas - download my cheat sheet. It covers the basics and has questions from the BBP listed on the bottom.


Fun with Parabolas

Email me any question

Hi - thanks for reading SAT - Tutor

If you can think of the problem, email it to me.

If you can sketch it & scan it all the better

My email address is phil@mccaffreytutoring.com

I'd love to hear from you

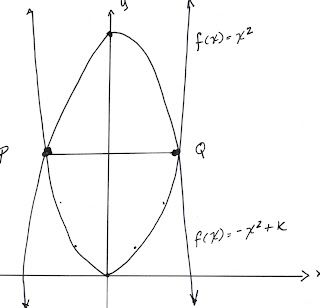
Symmetrical Parabola's: opposit "a"

Thanks for the feedback, come back and tell your friends. Sat-tutor is about to have a whole lot more, including practice problems and video explainations.

When two parabolas are defined by quadratic equations that have "opposite" coeffecients, the SAT is giving you a REALLY BIG clue. Looking something like:

f(x) = x^2

f(x) = -x^2 + k (where ^ is the symbol for exponent & k is a constant)

The SAT will give you points where these two intersect. Notice that they are both symmetrical about the Y-axis, making the two points of intersect equal distance from the Y-axis (where x = 0). Let's call those two points: P & Q

They give some clue about these two points, something like: the distance of line segment PQ is 6. What is the value of k?

First step:

The distance between PQ is important. Since the parabola's intersent at a point x, -x, the total distance between them, 2x is equal to 6. 2x = 6. x = 3, -x = -3

Second step:

Substitute x = 3, into the first equation. 3^2 = 9. The points of intersection P & Q are (3, 9) & (-3, 9)

Third step:

Substitute P or Q into the second equation: f(x) = -x^2 + k

9 = -(3)^2 + k

9 = -9 + k

18 = k

The one thing that I highly recommend SAT prep students is to buy "The Official Study Guide" published by The College Board. It has 8 practice tests from REAL SAT's. It is the only one that has REAL practice problems - so it is the best piece of intelligence.

I have my students go through and do every parabola problem in The Guide.

Check back in a few days and I will post all of the parabola problems in The Guide, with notation for "Symmetrical Parabola" problems.

Excuse the really crude drawing but it is now 3:30 in the morning. I had crashed in a chair after coming home from my night school class & was on my way to bed when I saw you had posted, so I cranked out this thought before I forgot it.

Now that I know how easy it is to make a drawing and post it - watch out!

Symmetrical Parabola's

The SAT loves to give a trick question: finding something out about a parabola by solving another puzzle first. More on this later - I just wanted to write down the idea so that I can come back and do it justice